1. Завдання № 1
2. Крок перший: вводимо змінні
3. Крок другий: складаємо і вирішуємо рівняння
4. Крок третій: знаходимо максимальне значення функції
5. нюанси рішення
6. Завдання № 2
7. Крок перший: вводимо змінні
8. Крок другий: складаємо і вирішуємо рівняння
9. Крок третій: знаходимо максимальне значення функції
10. Ключові моменти вирішення задач17 на продуктивність праці з ЄДІ з математики

Завдання цього типу з'явилися в ЄДІ відносно недавно, але застали зненацька як учнів, так і багатьох вчителів. А все тому що вирішуються вони за допомогою похідної - інструменту, абсолютно незвичного для другої частини іспиту.

Завдання 17. Григорій є власником двох заводів в різних містах. На заводах виробляються абсолютно однакові товари, але на заводі, розташованому в другому місті, використовується більш досконале обладнання. В результаті, якщо робочі на заводі, розташованому в першому місті, працюють сумарно $ {{t} ^ {2}} $ годин в тиждень, то за цей тиждень вони виробляють $ 3t $ одиниць товару; якщо робочі на заводі, розташованому в другому місті, працюють сумарно $ {{t} ^ {2}} $ годин в тиждень, то за цей тиждень вони виробляють $ 4t $ одиниць товару. За кожну годину роботи (на кожному із заводів) Григорій платить робітникові 500 рублів.

У наведеному умови є важливий момент, після усвідомлення якого у вас взагалі не буде проблем з вирішенням подібних завдань. Справа в тому, що величина $ t $, зазначена для першого заводу і для другого - це не одне і те ж число! Іншими словами, сумарний час робочих на першому і іншому заводі буде різним.

Для вирішення введемо нові змінні: $ {{a} ^ {2}} $ - сумарний час робочих на першому заводі, $ {{b} ^ {2}} $ - сумарний час на другому. З урахуванням продуктивності отримаємо:

$ \ Begin {align} & {{a} ^ {2}} \ to 3a \\ & {{b} ^ {2}} \ to 4b \\\ end {align} $

Таким чином, витративши сумарно $ {{a} ^ {2}} + {{b} ^ {2}} $ годин часу, ми отримаємо $ 3a + 4b $ одиниць продукції в тиждень. Все інше - елементарна математика, докладно описана в відеоуроці:

Минулого разу ми розглядали досить «неприємні» завдання, пов'язані з обчисленням часу в задачах про кредити. Але це було дуже просто в порівнянні з тим, що ми будемо розглядати сьогодні, а саме економічну задачу 17 про продуктивність праці, в якій потрібно застосовувати похідну. Ці завдання з'явилися в ЄДІ з математики відносно недавно, і ті, хто вже з ними зіткнувся, оцінили, що, по-перше, умова таких завдань досить довге, а, по-друге, в кожній з таких завдань є неприємна зачіпка, на якій «прогоріли» дуже багато учнів.

Думаю, ви вже здогадалися, що мова йде про ту саму завдання 17, коли у Григорія є два заводи, і ще вказана продуктивність праці, і потрібно оцінити, яку найбільшу кількість продукції можна зробити на цих двох заводах, якщо розподілити навантаження оптимально. Але насправді, в цих завданнях 17 немає нічого складного, навіть трохи простіше, ніж багато завдань на кредити. Тому зараз ми розглянемо одне з таких завдань, уважно пробіжить по кожному пункту і подивимося, як саме має виглядати ідеальне її рішення.

Завдання № 1

Григорій є власником двох заводів в різних містах. На заводах виробляються абсолютно однакові товари, але на заводі, розташованому в другому місті, використовується більш досконале обладнання. В результаті, якщо робочі на заводі, розташованому в першому місті, працюють сумарно $ {{t} ^ {2}} $ годин в тиждень, то за цей тиждень вони виробляють $ 3t $ одиниць товару; якщо робочі на заводі, розташованому в другому місті, працюють сумарно $ {{t} ^ {2}} $ годин в тиждень, то за цей тиждень вони виробляють $ 4t $. За кожну годину роботи (на кожному із заводів) Григорій платить робітникові 500 рублів.

Григорій готовий виділяти 5 000 000 рублів в тиждень на оплату праці робітників. Яку найбільшу кількість одиниць товару можна зробити за тиждень на цих двох заводах?

Крок перший: вводимо змінні

Перш за все, перед тим як переходити до безпосереднього вирішення завдання 17 з ЄДІ з математики, спробувати щось порахувати, скласти якісь формули, зрозумійте одну просту річ: величина $ {{t} ^ {2}} $, дана і в першому, і у другому реченні, ніяк не пов'язані один з одним. Коефіцієнт $ t $ нам дано виключно для того, щоб порівняти продуктивність на різних заводах при однаковій витраті часу. Думаю, це порівняння абсолютно очевидно: на першому продуктивність становить $ 3t $, а на другому - $ 4t $, тобто трохи більший. На практиці це означає наступне: давайте розпишемо, що відбувається на кожному з них.

На першому заводі у нас витрачається $ {{a} ^ {2}} $ часу (після заміни) і виробляється $ 3a $ одиниць продукції. На другому - $ {{b} ^ {2}} $ часу і $ 4b $ продукції.

А тепер давайте складемо витрати часу і сумарний випуск продукту.

Отримаємо, що сумарний витрата часу становить $ {{a} ^ {2}} + {{b} ^ {2}} $, а сумарний витрата продукції - $ 3a + 4b $. При цьому ще раз звертаю вашу увагу: ніхто не говорив, що $ {{a} ^ {2}} $ і $ {{b} ^ {2}} $ повинні бути рівні. Ключове слово тут «якщо» і в першому, і в другому випадку. Саме тому ми так сміливо міняємо коефіцієнти $ t $ на $ a $ в першому випадку і на $ b $ у другому випадку.

Крок другий: складаємо і вирішуємо рівняння

Давайте подивимося, що у нас вийшло. $ {{A} ^ {2}} + {{b} ^ {2}} $ - це сумарний витрата часу. Оскільки Григорій платить робітникові 500 рублів за кожну годину роботи, то найбільше він зможе заплатити таку суму:

\ [500 \ cdot \ left ({{a} ^ {2}} + {{b} ^ {2}} \ right) = 5000000 \]

Ось і перше рівняння.

Насправді, основна складність цього завдання 17 про продуктивність праці - зовсім не складання рівняння. Вона полягає в тому, що потрібно зрозуміти, що на першому і на другому заводі час різний. Саме тому для першого ми всюди замінили $ t $ на $ a $, а для другого - $ t $ на $ b $. В результаті як ви зараз побачите, ми отримаємо одне рівняння з двома невідомими, яке легко спрощується - одна невідома легко виражається через іншу. І тому вся функція, що виражає кількість виробленого товару, насправді залежить від однієї-єдиної змінної, в нашому випадку це буде змінна $ a $.

Далі, я думаю, все зрозуміло: у нас є функція, відрізок, на якому ця функція розглядається, а все, що нам потрібно знайти - це найбільше значення цієї функції на даному відрізку. Вообщем, класична задача для застосування похідних, в нашому випадку нове завдання 17 з ЄДІ з математики.

Сумарний випуск продукції ($ S $) дорівнює:

\ [S = 3a + 4b \ to \ max \]

Ось тепер завдання і проявилася: маючи обмеження на $ a $ і $ b $, нам потрібно добитися того, щоб $ S $ брала своє максимальне значення. Для початку давайте трошки попрацюємо з рівнянням: $$

\ [500 \ cdot \ left ({{a} ^ {2}} + {{b} ^ {2}} \ right) = 5000000 \ left | : 500 \ right. \]

\ [{{A} ^ {2}} + {{b} ^ {2}} = 10000 \]

Звідси висловимо $ b $:

\ [{{B} ^ {2}} = 10000 - {{a} ^ {2}} \]

\ [B = \ sqrt {10000 - {{a} ^ {2}}} \]

Звичайно, тут слід було б перед вираженням поставити $ \ pm $, проте у нас мова йде про час, а воно не може бути негативним, тому ми беремо позитивне значення. Разом сумарний обсяг виробленого товару може бути виписаний як функція від однієї-єдиної змінної $ a $:

\ [S = 3a + 4 \ sqrt {10000 - {{a} ^ {2}}} \]

Крок третій: знаходимо максимальне значення функції

Тепер нам потрібно знайти максимальне значення цієї функції на всій області визначення, а цілком очевидно, що величину $ a $, тобто кількість товару, випущеного на першому заводі, збільшувати до безкінечності не можна, просто тому що корінь має конкретну область визначення - величина, що стоїть під коренем, не повинна бути негативною. Давайте запишемо це:

\ [10000 - {{a} ^ {2}} \ ge 0 \]

\ [{{A} ^ {2}} \ le 10000 \]

\ [\ Left | a \ right | \ le 100 \]

\ [A \ in \ left [0; 100 \ right] \]

Разом ми отримали класичну задачу з першої частини ЄДІ з математики: у нас є функція, тобто інтервал, відповідно, потрібно знайти максимальне значення цієї функції на заданому інтервалі. Давайте вважати похідну:

\ [{S} '= 3 + 4 \ cdot \ frac {1 \ cdot \ left (10000 - {{a} ^ {2}} \ right)} {2 \ sqrt {10000 - {{a} ^ {2 }}}} = 3 + \ frac {4 \ cdot \ left (-2a \ right)} {2 \ sqrt {10000 - {{a} ^ {2}}}} = \]

\ [= 3 \ frac {4a} {\ sqrt {10000 - {{a} ^ {2}}}} \]

\ [3 \ frac {4a} {\ sqrt {10000 - {{a} ^ {2}}}} = 0 \]

Вирішуємо отримане рівняння:

\ [3 = \ frac {4a} {\ sqrt {\ sqrt {10000 - {{a} ^ {2}}}}} \]

\ [3 \ sqrt {10000 - {{a} ^ {2}}} = 4a \]

\ [9 \ left (10000 - {{a} ^ {2}} \ right) = 16 {{a} ^ {2}} \]

\ [90000-9 {{a} ^ {2}} = 16 {{a} ^ {2}} \]

\ [25 {{a} ^ {2}} = 90000 \]

\ [5a = 3 \ cdot 100 \]

\ [A = \ frac {3 \ cdot 100} {5} = 60 \]

Тепер, знаючи, чому дорівнює $ a $, легко знайти $ b $:

\ [B = \ sqrt {10000-3600} = \ sqrt {6400} = 80 \]

Однак для повного і обгрунтованого рішення необхідно зрозуміти знак похідної. Давайте накреслив числову пряму і відзначимо на ній $ a = 60 $ і подивимося, що відбувається при $ a> 60 $:

Наприклад, якщо взяти $ a = 99 $ ми отримаємо наступне:

\ [10000 - {{99} ^ {2}} = {{100} ^ {2}} - {{99} ^ {2}} = \ left (100-99 \ right) \ left (100 + 99 \ right) = 199 \]

Якщо подивимося на вихідне вираз, то очевидно, що $ \ sqrt {199} <99 $, але порахувавши його, отримуємо у відповіді негативне число.

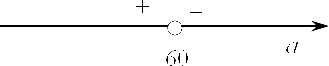
Звідси випливає, що $ a = 60 $ є точкою максимуму, тобто саме тієї, яку ми і хотіли знайти. Саме в ній наша початкова функція приймає початкове значення. Залишилося підставити в $ S $ отримане значення $ a $ і $ b $:

\ [S = 3 \ cdot 60 + 4 \ cdot 80 = 180 + 320 = 500 \]

Відповідь: 500 одиниць товару.

нюанси рішення

Як бачите, все виявилося не так вже й складно. Єдино, що нам потрібно запам'ятати - це те, що величина $ {{t} ^ {2}} $, коли мова йде про перший заводі дає нам інформацію про продуктивність праці саме на ньому, тобто пов'язує час, витрачений на виробництво і кількість продукції в рамках тільки нього.

Величина $ {{t} ^ {2}} $, що відноситься до другого заводу, каже нам саме про нього і ніяк не пов'язана з першим.

Більш того, вважати, що кількість часу, витраченого робітниками на першому і на другому заводах, абсолютно однаково - це взагалі дурість, тому що в цьому випадку отримане рівняння виявилося б набагато простіше і вирішувалося б як елементарне лінійне: нам би не треба було ніяких похідних, ніяких доказів, що ми отримали точку максимуму - ми просто б розділили зарплату між робітниками першого і другого виробництв навпіл.

Тому запам'ятайте: час, витрачений на першому і на другому заводах, різний, тому нехай на першому витрачено $ {{a} ^ {2}} $ часу, а на другому - $ {{b} ^ {2}} $. У цьому випадку завдання дійсно стає складніше, при цьому цікавіше і цілком гідною називатися завданням 17 з ЄДІ з математики.

Завдання № 2

А в якості десерту пропоную вирішити ще одну таку ж задачу 17 з ЄДІ з математики, однак викладки в цей раз будуть мінімальними, по можливості такими, які і потрібно робити на іспиті з математики.

Сергій володіє двома промисловими заводами, що випускають однакову продукцію. На другому заводі встановлено сучасне обладнання, тому на ньому може бути випущено більше одиниць продукції. Відомо, що якщо робочі першого заводу сумарно трудяться $ {{t} ^ {2}} $ годин в тиждень, то випускають $ t $ одиниць продукції. А якщо робочі другого заводу сумарно трудяться $ {{t} ^ {2}} $ годин в тиждень, то випускають $ 2t $ одиниць продукції. Ставка заробітної плати робітника становить 500 рублів на годину.

Сергій готовий платити робітникам 30 250 000 рублів в тиждень. На яку максимальну кількість одиниць продукції він може розраховувати?

Крок перший: вводимо змінні

Якщо робочі на першому заводі трудяться $ {{x} ^ {2}} $, то це дає нам $ x $ одиниць товару. На другому $ {{y} ^ {2}} $ часу дає нам $ y $ товарів. Знову складаємо витрати часу - $ {{x} ^ {2}} + {{y} ^ {2}} $ і окремо складаємо обсяг продукції - $ x + 2y $. Величина $ {{x} ^ {2}} + {{y} ^ {2}} $ - це сумарний витрата часу за тиждень.

Крок другий: складаємо і вирішуємо рівняння

Оскільки за кожну годину роботи сплачується 500 рублів, то сумарний витрата грошей за тиждень складе:

\ [500 \ cdot \ left ({{x} ^ {2}} + {{y} ^ {2}} \ right) = 30250000 \]

\ [{{X} ^ {2}} + {{y} ^ {2}} = 60500 \]

Таким способом, обмеження на $ {{x} ^ {2}} $ і $ {{y} ^ {2}} $ знайдені.

Тепер необхідно записати суму:

\ [S = x + 2y \ to \ max \]

Знову ж будемо вважати похідну, але для цього спочатку необхідно висловити $ y $ через $ x $:

\ [{{Y} ^ {2}} = 60500 - {{x} ^ {2}} \]

\ [Y = \ sqrt {60500 - {{x} ^ {2}}} \]

Підставляємо знайдене значення $ y $ в нашу формулу і отримуємо:

\ [S = x + 2 \ cdot \ sqrt {60500 - {{x} ^ {2}}} \]

Знаходимо похідну цієї конструкції:

\ [{S} '= 1 + 2 \ frac {1 \ left (-2x \ right)} {2 \ sqrt {60500 - {{x} ^ {2}}}} = 1 \ frac {2x} { \ sqrt {60500 - {{x} ^ {2}}}} \]

Знову прирівнюємо отриманий вираз до нуля:

\ [1 \ frac {2x} {\ sqrt {60500 - {{x} ^ {2}}}} = 0 \]

\ [\ Frac {1} {1} = \ frac {2x} {\ sqrt {60500 - {{x} ^ {2}}}} \]

\ [\ Sqrt {60500 - {{x} ^ {2}}} = 2x \]

\ [60500 - {{x} ^ {2}} = 4 {{x} ^ {2}} \]

\ [60500 = 5 {{x} ^ {2}} \]

\ [{{X} ^ {2}} = \ frac {60500} {5} = 121 \ cdot 100 \]

\ [X = 11 \ cdot 10 = 110 \]

Крок третій: знаходимо максимальне значення функції

Ми отримали критичну точку функції $ S $. Тепер необхідно довести, що це точка максимуму. Для цього накреслив знову пряму, відзначимо на ній отриману точку 110 і візьмемо будь-яке число, більше ніж 110. Однак для спрощення подальших викладок пропоную взяти не рандомноє число як в минулий раз, а порахувати його за допомогою наступного методу. Для початку давайте знайдемо $ y $. Запишемо такий вислів:

\ [Y = 2x = 220 \]

Очевидно, що 220 більше 110, і якщо ми поставимо його в нашу функцію, то отримаємо число на зазначеному інтервалі:

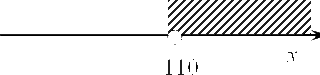
Давайте підставимо:

$ {S} '\ left (220 \ right) = 1 \ frac {2 \ cdot 220} {\ sqrt {60500 - {{220} ^ {2}}}} = 1 \ frac {440} {\ sqrt {60500-48400}} = $

$ = 1 \ frac {440} {\ sqrt {12100}} = 1 \ frac {440} {110} = 1-4 = -3 $

Отже, справа від числа 110 ми отримуємо негативну похідну, а зліва, природно, буде позитивна.

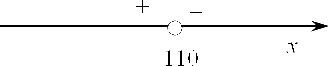
Разом 110 - точка максимуму. Це є строгим обгрунтуванням.

Тепер підставляємо у вираз $ x $ і $ y $, які ми знайшли:

\ [S = 110 + 2 \ cdot 220 = 110 + 440 = 550 \]

Відповідь: 550 одиниць товару.

Ключові моменти вирішення задач17 на продуктивність праці з ЄДІ з математики

Все, що нам потрібно знати - це:

1. Правило обчислення похідних складних функцій.
2. Правила вирішення нескладних рівнянь.

Крім того, хотів би відзначити, що не треба боятися працювати з великими числами. Такі вирази, коли у нас з'являються п'ятизначні і більш числа, абсолютно типові для останніх завдань 17 з ЄДІ з математики, тому що вони реально важкі. Але насправді, в цих завданнях з ЄДІ немає нічого важкого. Вам тільки потрібно знати наступне:

• $ {{A} ^ {2}} \ to a $ і $ {{b} ^ {2}} \ to 2b $ - як пов'язано витрачений час з об'ємом випущеного товару;
• $ S = a + 2b \ to \ max $ - сумарний обсяг товару знаходиться за нескладною формулою.

Крім того, необхідно розуміти, як пов'язано час, витрачений на першому виробництві і на другому, тобто які максимальні обмеження на цей час.

А далі справа техніки: вважаємо похідну, вирішуємо рівняння, підставляємо у вихідне обмеження і отримуємо остаточну відповідь.

Сподіваюся, це відео допоможе вам побудувати власний завод, де ви будете платити робітникам по 30 млн. Рублів в тиждень, якщо такої суми вам виявиться недостатньо, заходите на наш сайт, підписуйтесь на паблік ВКонтакте і на канал в YouTube. До нової зустрічі!

Дивіться також:

1. Як правильно складати рівняння в завданнях про кредити з ЄДІ з математики
2. Завдання з економічним змістом - основні формули
3. Пробний ЄДІ-2011 з математики, варіант №8
4. Пробний ЄДІ 2012. Варіант 1 (без логарифмів)
5. Тест: найпростіші показникові рівняння (2 варіант)
6. Текстові завдання про рейки